2024北京高考数学试题

绝密★本科目考试启用前

2024年普通高等学校招生全国统一考试数学试题（北京卷）

本试卷共12页，150分.考试时长120分钟.考生务必将答案答在答题卡上，在试卷上作答无效.考试结束后，将本试卷和答题卡一并交回.

第一部分（选择题  共40分）

一、选择题共10小题，每小题4分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项．

1. 已知集合，，则（    ）

A.  B.

C.  D.

2. 已知，则（    ）．

A.  B.  C.  D. 1

3. 求圆的圆心到的距离（    ）

A.  B. 2 C.  D.

4. 的二项展开式中的系数为（    ）

A. 15 B. 6 C.  D.

5. 已知向量，，则“”是“或”的（    ）条件．

A. 必要而不充分条件 B. 充分而不必要条件

C. 充分且必要条件 D. 既不充分也不必要条件

6 已知，，，，则（    ）

A. 1 B. 2 C. 3 D. 4

7. 记水质量为，并且d越大，水质量越好．若S不变，且，，则与的关系为（    ）

A.

B.

C. 若，则；若，则；

D. 若，则；若，则；

8. 已知以边长为4的正方形为底面的四棱锥，四条侧棱分别为4，4，，，则该四棱锥的高为（    ）

A.  B.  C.  D.

9. 已知，是函数图象上不同的两点，则下列正确的是（    ）

A.  B.

C.  D.

10. 若集合表示的图形中，两点间最大距离为d、面积为S，则（    ）

A. ， B. ，

C. ， D. ，

第二部分（非选择题  共110分）

二、填空题共5小题，每小题5分，共25分.

11. 已知抛物线，则焦点坐标为________．

12. 已知，且α与β的终边关于原点对称，则的最大值为________．

13. 已知双曲线，则过且和双曲线只有一个交点的直线的斜率为________．

14. 已知三个圆柱体积为公比为10的等比数列．第一个圆柱的直径为65mm，第二、三个圆柱的直径为325mm，第三个圆柱的高为230mm，求前两个圆柱的高度分别为________．

15. 已知，，不为常数列且各项均不相同，下列正确的是______.

①，均为等差数列，则M中最多一个元素；

②，均为等比数列，则M中最多三个元素；

③为等差数列，为等比数列，则M中最多三个元素；

④单调递增，单调递减，则M中最多一个元素

三、解答题共6小题，共85分.解答应写出文字说明，演算步骤或证明过程.

16. 在△ABC中，，A为钝角，．

（1）求；

（2）从条件①、条件②和条件③这三个条件中选择一个作为已知，求△ABC的面积．

①；②；③．

注：如果选择条件①、条件②和条件③分别解答，按第一个解答计分．

17. 已知四棱锥P-ABCD，，，，，E是上一点，．

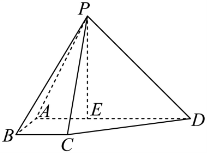
（1）若FPE中点，证明：平面．

（2）若平面，求平面与平面夹角的余弦值．

18. 已知某险种的保费为万元，前3次出险每次赔付万元，第4次赔付万元

在总体中抽样100单，以频率估计概率：

（1）求随机抽取一单，赔偿不少于2次的概率；

（2）（i）毛利润是保费与赔偿金额之差．设毛利润为，估计的数学期望；

（ⅱ）若未赔偿过的保单下一保险期的保费下降，已赔偿过的增加．估计保单下一保险期毛利润的数学期望．

19. 已知椭圆方程C：，焦点和短轴端点构成边长为2的正方形，过的直线l与椭圆交于A，B，，连接AC交椭圆于D．

（1）求椭圆方程和离心率；

（2）若直线BD的斜率为0，求t．

20. 已知在处切线为l．

（1）若切线l的斜率，求单调区间；

（2）证明：切线l不经过；

（3）已知，，，，其中，切线l与y轴交于点B时．当，符合条件的A的个数为？

（参考数据：，，）

21. 设集合．对于给定有穷数列A和序列Ω：，，···，，，定义变换T：将数列A的第，，，列加1，得到数列；将数列的第，，，列加1，得到数列…；重复上述操作，得到数列，记为Ω（A）．若为偶数，证明：“Ω（A）为常数列”的充要条件为“”．