有途教育热门推荐
天津高考数学试题及答案解析汇总
天津高考数学试题及答案解析汇总
天津高考数学试题及答案解析汇总
天津高考数学试题及答案解析汇总
2024年天津成人高考准考证打印时间 具体在什么时候
2024年天津成人高考报名照片要求 用什么底色
天津成考报名时间2024具体时间 日期是哪天
2024年天津成考报名截止时间 具体几号结束报考
天津2025上半年自学考试报名具体截止到几号
今年的高考已经结束，相信很多同学都开始过上了愉快的暑假生活。但是这并不意味着可以完全放松了，部分考生已经开始进行高考估分了，以便于可以更好地填报志愿。小编也整理了2024天津高考数学试卷及答案解析，供各位考生参考。
2024天津高考数学考试试卷及答案【考后更新】
高考落下帷幕后考生就要准备志愿填报的工作了，下面是天津地区数学科目高考试题的具体内容，供大家估分参考：
| 高考地区 | 考试科目 | 试题 | 答案解析 |
| 天津 | 数学 | 点击查看 | 点击查看 |
高考估分是有必要的，高考估分不是为了让你知道自己大概能够考出多少分，而是让你知道自己高考成绩、全省排名的大致范围，以便于自己可以更好地填报志愿。
天津高考后哪些学生不适合估分
第一类：记忆力不好的学生
天津高考的答题卡、试卷、草纸都是统一回收的，学生想要记住自己全部的答案其实并不太容易，如果学生没有记答案的习惯，或记忆力不太好，那么估分其实是没有什么意义的。
估分估高了，天津学生和家长可能会白欢喜一场;估分估低了，又会影响学生和家长的情绪，这种情况下家长最好还是不要勉强了。
第二类：心态较差的学生
还有一类学生也不适合估分，那就是心态比较差的学生，众所周知高三一年对于天津学生来说是非常累的，很多学生心理压力都很大。
如果学生本身心态不算很好，那么最好不要强制他们估分，可以适当让孩子出去放松一下，减轻他们的心理压力，半个月以后高考成绩自然会出来。
绝密 ★ 启用前
2024年普通高等学校招生全国统一考试（新课标I卷）
数学
本试卷共10页，19小题，满分150分.
注意事项：
1.答题前，先将自己的姓名、准考证号、考场号、座位号填写在试卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置.
2.选择题的作答：每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑.写在试卷、草稿纸和答题卡上的非答题区域均无效.
3.填空题和解答题的作答：用黑色签字笔直接答在答题卡上对应的答题区域内.写在试卷、草稿纸和答题卡上的非答题区域均无效.
4.考试结束后，请将本试卷和答题卡一并上交.
一、选择题：本题共 8 小题，每小题 5 分，共 40 分. 在每小题给出的四个选项中，只有一个选项是正确的．请把正确的选项填涂在答题卡相应的位置上.
1. 已知集合
，则
（ ）
A. 
B. 
C. 
D. 
2
若
，则
（ ）
A. 
B. 
C. 
D. 
3. 已知向量
，若
，则
（ ）
A. 
B. 
C. 1 D. 2
4. 已知
，则
（ ）
A. 
B. 
C. 
D. 
5. 已知圆柱和圆锥的底面半径相等，侧面积相等，且它们的高均为
，则圆锥的体积为（ ）
A. 
B. 
C. 
D. 
6. 已知函数为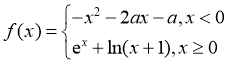
，在R上单调递增，则a取值的范围是（ ）
A. 
B. 
C. 
D. 
7. 当
时，曲线
与
的交点个数为（ ）
A. 3 B. 4 C. 6 D. 8
8. 已知函数为
的定义域为R，
，且当
时
，则下列结论中一定正确的是（ ）
A. 
B. 
C. 
D. 
二、选择题：本题共 3 小题，每小题 6 分，共 18 分. 在每小题给出的选项中，有多项符合题目要求. 全部选对得 6 分，部分选对的得部分分，选对但不全的得部分分，有选错的得0分.
9. 为了解推动出口后的亩收入（单位：万元）情况，从该种植区抽取样本，得到推动出口后亩收入的样本均值
，样本方差
，已知该种植区以往的亩收入
服从正态分布
，假设推动出口后的亩收入
服从正态分布
，则（ ）（若随机变量Z服从正态分布
，
）
A 
B. 
C. 
D. 
10. 设函数
，则（ ）
A. 
是的极小值点 B. 当
时，
C. 当
时，
D. 当
时，
11. 造型
可以做成美丽的丝带，将其看作图中曲线C的一部分.已知C过坐标原点O.且C上的点满足横坐标大于，到点
的距离与到定直线
的距离之积为4，则（ ）
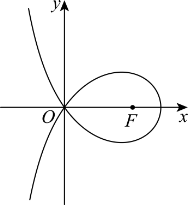
A. 
B. 点
在C上
C. C在第一象限的点的纵坐标的最大值为1 D. 当点
在C上时，
三、填空题：本题共 3 小题，每小题 5 分，共 15 分.
12. 设双曲线
左右焦点分别为
，过
作平行于
轴的直线交C于A，B两点，若
，则C的离心率为___________．
13. 若曲线
在点
处的切线也是曲线
的切线，则
__________.
14. 甲、乙两人各有四张卡片，每张卡片上标有一个数字，甲的卡片上分别标有数字1，3，5，7，乙的卡片上分别标有数字2，4，6，8，两人进行四轮比赛，在每轮比赛中，两人各自从自己持有的卡片中随机选一张，并比较所选卡片上数字的大小，数字大的人得1分，数字小的人得0分，然后各自弃置此轮所选的卡片（弃置的卡片在此后的轮次中不能使用）.则四轮比赛后，甲的总得分不小于2的概率为_________.
四、解答题：本题共 5 小题，共 77 分. 解答应写出文字说明、证明过程或演算步骤.
15. 记
内角A、B、C的对边分别为a，b，c，已知
，
（1）求B；
（2）若面积为
，求c．
16. 已知
和
为椭圆
上两点.
（1）求C的离心率;
（2）若过P的直线
交C于另一点B，且
的面积为9，求的方程．
17. 如图，四棱锥
中，
底面ABCD，
，
．
（1）若
，证明：
平面
；
（2）若
，且二面角
的正弦值为
，求
．
18. 已知函数
（1）若
，且
，求
的最小值；
（2）证明：曲线
中心对称图形；
（3）若
当且仅当，求
的取值范围．
19. 设m为正整数，数列
是公差不为0的等差数列，若从中删去两项
和
后剩余的
项可被平均分为
组，且每组的4个数都能构成等差数列，则称数列是
可分数列．
（1）写出所有的
，
，使数列
是可分数列；
（2）当
时，证明：数列是
可分数列；
（3）从
中一次任取两个数
和
，记数列是可分数列的概率为
，证明：
．