热门推荐

2022初中生寒假放假时间表一览

2022年中小学期末考试时间安排

2019中考政策 都有哪些

2020合肥中考成绩何时发布

2020年河南中考成绩什么时候出

中考数学必考知识点

2020安徽中考成绩查询日期

2020年宜宾中考总分多少

2020中考成绩总分


青岛市二〇一七年初中学业水平考试
数学试题
一、2017年青岛市中考数学试题选择题:
1.![]() 的相反数是( )
的相反数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.下列四个图形中,是轴对称图形,但不是中心对称图形的是( )
 3.小明家1至6月份的用水量统计如图所示,关于这组数据,下列说法中错误的是( )
3.小明家1至6月份的用水量统计如图所示,关于这组数据,下列说法中错误的是( )
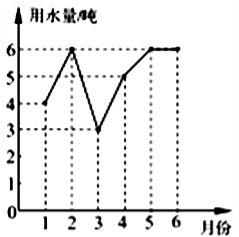
A.众数是6吨 B.平均数是5吨 C.中位数是5吨 D.方差是![]()
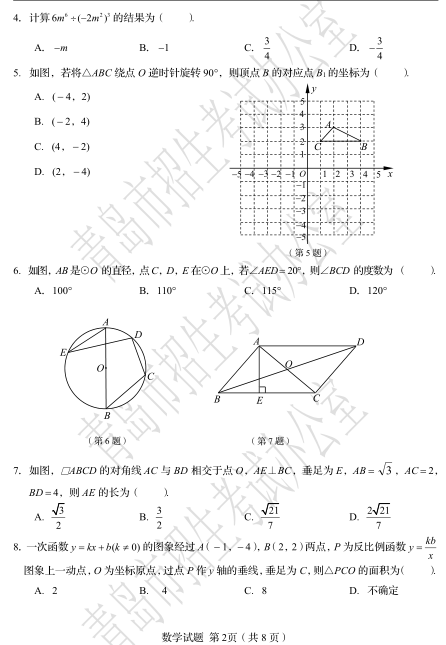
4.计算![]() 的结果为( )
的结果为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.如图,若将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,则顶点
,则顶点![]() 的对应
的对应![]() 的坐标为( )
的坐标为( )
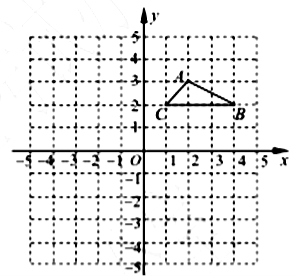
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.如图,![]() 是⊙
是⊙![]() 的直径,点
的直径,点![]() 在⊙
在⊙![]() 上,若
上,若![]() ,则
,则![]() 的度数为( )
的度数为( )
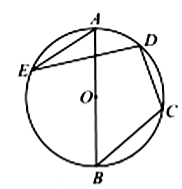
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
7.如图,□![]() 的对角线
的对角线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,垂足为
,垂足为![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() 的长为( )
的长为( )
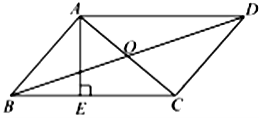
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.一次函数![]() 的图象经过
的图象经过![]() ,
,![]() 两点,
两点,![]() 为反比例函数
为反比例函数![]() 图象上一动点,
图象上一动点,![]() 为坐标原点,过点
为坐标原点,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,则
,则![]() 的面积为( )
的面积为( )
A.2 B.4 C. 8 D.不确定
二、2017年青岛市中考数学试题填空题
9. 近年来,国家重视精准扶贫,收效显著,据统计约65000000人脱贫.65000000用科学记数法可表示为 .
10.计算:![]() .
.
11.若抛物线![]() 与
与![]() 轴没有交点,则
轴没有交点,则![]() 的取值范围是 .
的取值范围是 .
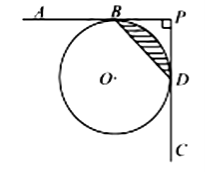
12.如图,直线![]() 分别与⊙
分别与⊙![]() 相切于
相切于![]() 两点,且
两点,且![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,若
,若![]() ,则阴影部分的面积为 .
,则阴影部分的面积为 .
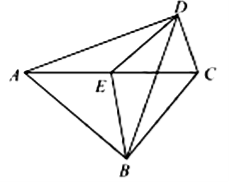
13.如图,在四边形![]() 中,
中,![]() ,
,![]() 为对角线
为对角线![]() 的中点,连接
的中点,连接![]() ,若
,若![]() ,则
,则![]() 的度数为 度.
的度数为 度.
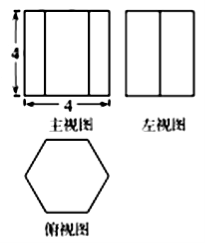
14.已知某几何体的三视图如图所示,其中俯视图为正六边形,则该几何体的表面积为 .
三、2017年青岛市中考数学试题作图题
用圆规、直尺作图,不写作法,但要保留作图痕迹
15.已知:四边形![]() .
.
求作:点![]() ,使
,使![]() ,且点
,且点![]() 到边
到边![]() 和
和![]() 的距离相等.
的距离相等.

四、2017年青岛市中考数学试题解答题
16.(1)解不等式组: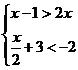
(2)化简:![]()
17.小华和小军做摸球游戏:![]() 袋装有编号为1,2,3的三个小球,
袋装有编号为1,2,3的三个小球,![]() 袋装有编号为4,5,6的三个小球,两袋中的所有小球除编号外都相同.从两个袋子中分别随机摸出一个小球,若
袋装有编号为4,5,6的三个小球,两袋中的所有小球除编号外都相同.从两个袋子中分别随机摸出一个小球,若![]() 袋摸出小球的编号与
袋摸出小球的编号与![]() 袋摸出小球的编号之差为偶数,则小华胜,否则小军胜.这个游戏对双方公平吗?请说明理由.
袋摸出小球的编号之差为偶数,则小华胜,否则小军胜.这个游戏对双方公平吗?请说明理由.
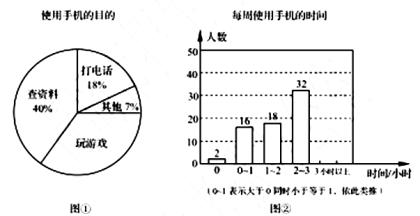
18.某中学开展了“手机伴我健康行”主题活动.他们随机抽取部分学生进行“使用手机的目的”和“每周使用手机的时间”的问卷调查,并绘制成如图①,②的统计图.已知“查资料”的人数是40人.
请你根据以上信息解答下列问题:
(1)在扇形统计图中,“玩游戏”对应的圆心角度数是 度;
(2)补全条形统计图;
(3)该校有学生1200人,估计每周使用手机时间在2小时以上(不含2小时)的人数.
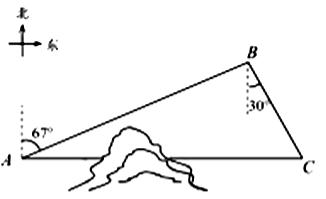
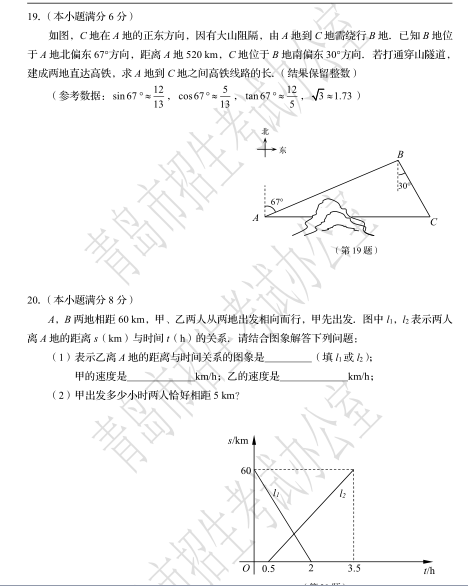
19.如图,![]() 地在
地在![]() 地的正东方向,因有大山阻隔,由
地的正东方向,因有大山阻隔,由![]() 地到
地到![]() 地需绕行
地需绕行![]() 地.已知
地.已知![]() 地位于
地位于![]() 地北偏东
地北偏东![]() 方向,距离
方向,距离![]() 地520
地520![]() ,
,![]() 地位于
地位于![]() 地南偏东
地南偏东![]() 方向.若打通穿山隧道,建成两地直达高铁,求
方向.若打通穿山隧道,建成两地直达高铁,求![]() 地到
地到![]() 地之间高铁线路的长.(结果保留整数)
地之间高铁线路的长.(结果保留整数)
(参考数据:![]() )
)
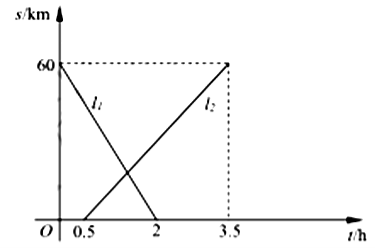
20.![]() 两地相距
两地相距![]() ,甲、乙两从两地出发相向而行,甲先出发.图中
,甲、乙两从两地出发相向而行,甲先出发.图中![]() 表示两人离
表示两人离![]() 地的距离
地的距离![]() 与事件
与事件![]() 的关系.请结合图象解答下列问题:
的关系.请结合图象解答下列问题:
(1)表示乙离![]() 地的距离与时间关系的图象是 (填
地的距离与时间关系的图象是 (填![]() 或
或![]() );甲的速度是
);甲的速度是 ![]() ;乙的速度是
;乙的速度是 ![]() ;
;
(2)甲出发多少小时两人恰好相距![]() ?
?
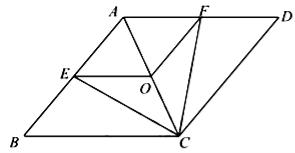
21.已知:如图,在菱形![]() 中,点
中,点![]() 分别为
分别为![]() 的中点,连接
的中点,连接![]() .
.
(1)求证:![]() ≌
≌![]() ;
;
(2)当![]() 与
与![]() 满足什么关系时,四边形
满足什么关系时,四边形![]() 是正方形?请说明理由.
是正方形?请说明理由.
22.青岛市某大酒店豪华间实行淡季、旺季两种价格标准,旺季每间价格比淡季上涨![]() .下表是去年该酒店豪华间某两天的相关记录:
.下表是去年该酒店豪华间某两天的相关记录:
| 淡季 | 旺季 |
未入住房间数 | 10 | 0 |
日总收入(元) | 24000 | 40000 |
(1)该酒店豪华间有多少间?旺季每间价格为多少元?
(2)今年旺季来临,豪华间的间数不变.经市场调查发现,如果豪华间仍旧实行去年旺季价格,那么每天都客满;如果价格继续上涨,那么每增加25元,每天未入住房间数增加1间.不考虑其他因素,该酒店将豪华间的价格上涨多少元时,豪华间的日总收入最高?最高日总收入是多少元?
23.数和形是数学的两个主要研究对象,我们经常运用数形结合、数形转化的方法解决一些数学问题.下面我们来探究“由数思形,以形助数”的方法在解决代数问题中的应用.
探究一:求不等式![]() 的解集
的解集
(1)探究![]() 的几何意义
的几何意义
如图①,在以![]() 为原点的数轴上,设点
为原点的数轴上,设点![]() 对应的数是
对应的数是![]() ,有绝对值的定义可知,点
,有绝对值的定义可知,点![]() 与点
与点![]() 的距离为
的距离为![]() ,可记为
,可记为![]() .将线段
.将线段![]() 向右平移1个单位得到线段
向右平移1个单位得到线段![]() ,此时点
,此时点![]() 对应的数是
对应的数是![]() ,点
,点![]() 对应的数是1.因为
对应的数是1.因为![]() ,所以
,所以![]() ,因此,
,因此,![]() 的几何意义可以理解为数轴上
的几何意义可以理解为数轴上![]() 所对应的点
所对应的点![]() 与1所对应的点
与1所对应的点![]() 之间的距离
之间的距离![]() .
.
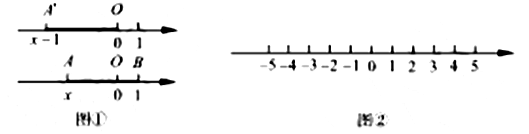
(2)求方程![]() 的解
的解
因为数轴上3和![]() 所对应的点与1所对应的点之间的距离都为2,所以方程的解为
所对应的点与1所对应的点之间的距离都为2,所以方程的解为![]() ,
,![]() .
.
(3)求不等式![]() 的解集
的解集
因为![]() 表示数轴上
表示数轴上![]() 所对应的点与1所对应的点之间的距离,所以求不等式解集就转化为求这个距离小于2的点对应的数
所对应的点与1所对应的点之间的距离,所以求不等式解集就转化为求这个距离小于2的点对应的数![]() 的范围.
的范围.
请在图②的数轴上表示![]() 的解集,并写出这个解集.
的解集,并写出这个解集.
探究二:探究![]() 的几何意义
的几何意义
(1)探究![]() 的几何意义
的几何意义
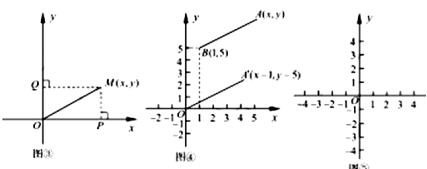
如图③,在直角坐标系中,设点![]() 的坐标为
的坐标为![]() ,过
,过![]() 作
作![]()
![]() 轴于
轴于![]() ,作
,作![]() 轴于
轴于![]() ,则
,则![]() 点坐标为
点坐标为![]() ,
,![]() 点坐标为
点坐标为![]() ,
,![]() ,
,![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,因此,
,因此,![]() 的几何意义可以理解为点
的几何意义可以理解为点![]() 与点
与点![]() 之间的距离
之间的距离![]() .
.
(2)探究![]() 的几何意义
的几何意义
如图④,在直角坐标系中,设点![]() 的坐标为
的坐标为![]() ,由探究二(1)可知,
,由探究二(1)可知,![]() ,将线段
,将线段![]() 先向右平移1个单位,再向上平移5个单位,得到线段
先向右平移1个单位,再向上平移5个单位,得到线段![]() ,此时点
,此时点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,因为
,因为![]() ,所以
,所以![]() ,因此
,因此![]() 的几何意义可以理解为点
的几何意义可以理解为点![]() 与点
与点![]() 之间的距离
之间的距离![]() .
.
(3)探究![]() 的几何意义
的几何意义
请仿照探究二(2)的方法,在图⑤中画出图形,并写出探究过程.
(4)![]() 的几何意义可以理解为: .
的几何意义可以理解为: .
拓展应用:
(1)![]() 的几何意义可以理解为:点
的几何意义可以理解为:点![]() 与点
与点![]() 的距离和点
的距离和点![]() 与点
与点![]() (填写坐标)的距离之和.
(填写坐标)的距离之和.
(2)![]() 的最小值为 .(直接写出结果)
的最小值为 .(直接写出结果)
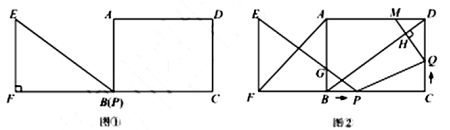
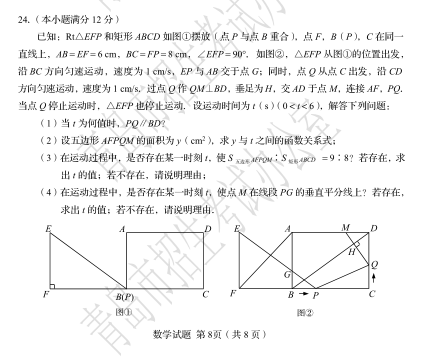
24.已知:![]() 和矩形
和矩形![]() 如图①摆放(点
如图①摆放(点![]() 与点
与点![]() 重合),点
重合),点![]() ,
,![]() 在同一直线上,
在同一直线上,![]() ,
,![]() ,
,![]() .如图②,
.如图②,![]() 从图①的位置出发,沿
从图①的位置出发,沿![]() 方向匀速运动,速度为1
方向匀速运动,速度为1![]() ,
,![]() 与
与![]() 交于点
交于点![]() ;同时,点
;同时,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为1
方向匀速运动,速度为1![]() .过点
.过点![]() 作
作![]() ,垂足为
,垂足为![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,当点
,当点![]() 停止运动时,
停止运动时,![]() 也停止运动.设运动事件为
也停止运动.设运动事件为![]() .www.ccutu.com解答下列问题:
.www.ccutu.com解答下列问题:
(1)当![]() 为何值时,
为何值时,![]() ?
?
(2)设五边形![]() 的面积为
的面积为![]() (
(![]() ),求
),求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)在运动过程中,是否存在某一时刻![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(4)在运动过程中,是否存在某一时刻![]() ,使点
,使点![]() 在线段
在线段![]() 的垂直平分线上?若存在,求出
的垂直平分线上?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
![C:\Users\Administrator\AppData\Roaming\Tencent\Users\1811767589\QQ\WinTemp\RichOle\07)PP1GC}YRV8]PL8HI7SNC.png](http://img.ccutu.com/upLoad/doc20170809/565659ud/151105.250.png)
![C:\Users\Administrator\AppData\Roaming\Tencent\Users\1811767589\QQ\WinTemp\RichOle\__~~43L7HUL7]952G5~ZHY4.png](http://img.ccutu.com/upLoad/doc20170809/565659ud/151105.252.png)
![C:\Users\Administrator\AppData\Roaming\Tencent\Users\1811767589\QQ\WinTemp\RichOle\9FV]QN[61O1HP{2(GEN]7]M.png](http://img.ccutu.com/upLoad/doc20170809/565659ud/151105.253.png)
影子题
|
![C:\Users\Administrator\AppData\Roaming\Tencent\Users\1811767589\QQ\WinTemp\RichOle\5DYG~NN3U~SV1`]UXIK(IBI.png](http://img.ccutu.com/upLoad/doc20170809/565659ud/151105.256.png)

|


影子题
|
影子题
|
![]()









